Changer mes Données
Changer mon Mot de Passe
Se Déconnecter
Boite de Réception
Messages Envoyés
Brouillons
Nouveau MessageCombo : Pouce de Krark + Mana Screw (Mana infini)
Rubrique Combos
Informations
Etat : Refusée
Date : 05/09/2017 à 09:54
Auteur : super
Lecture : 2082
Nombre de commentaire : 6
Validé par : knight_seb
Fiche du Membre
Hors Ligne
Membre Actif
Grade : [Seigneur] 
Inscrit le 04/06/2003
Dernière connexion : aujourd'hui, il y a 4h
5514 Messages/ 0 Contributions/ 168 Pts
Message PrivéModérateurs combos
Modérateur
Pouce de Krark
Texte Anglais
Krark's Thumb 
Legendary Artifact
If you would flip a coin, instead flip two coins and ignore one.
Legendary Artifact
If you would flip a coin, instead flip two coins and ignore one.
Texte Français
Pouce de Krark
Artefact légendaire
Si vous deviez jouer à pile ou face, lancez à la place deux pièces et ignorez l'une d'elles.
Artefact légendaire
Si vous deviez jouer à pile ou face, lancez à la place deux pièces et ignorez l'une d'elles.
Infos sur cette Carte Magic
Disponibilités :
7 Decks utilisent cette carte
0 Combo utilise cette carte
Aucune Analyse de cette carte
Mana Screw
Texte Anglais
Mana Screw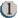 
Artifact
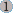: Flip a coin. If you win the flip, add 
to your mana pool. Play this ability only any time you could cast an instant.
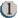
Artifact
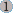: Flip a coin. If you win the flip, add to your mana pool. Play this ability only any time you could cast an instant.
Texte Français
(n'existe pas en français)
Artefact
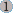: Jouez à pile ou face. Si vous gagnez, ajoutez à votre réserve. Ne jouez cette capacité que lorsque vous pourriez lancerun éphémère.
Artefact
: Jouez à pile ou face. Si vous gagnez, ajoutez à votre réserve. Ne jouez cette capacité que lorsque vous pourriez lancerun éphémère.
Infos sur cette Carte Magic
Disponibilités :
0 Deck utilise cette carte
0 Combo utilise cette carte
Aucune Analyse de cette carte
Explication de la Combinaison par l'auteur
Voici une combo pour les matheux, qui permet de produire de grandes quantités de mana, le plus souvent une quantité arbitrairement grande de mana, c'est-à-dire de faire mana infini.
Attention: cette explication contient des maths de niveau maths sup.
Le principe est simple. Mana Screw vous permet, en payant 1 mana, de lancer une pièce. Si vous gagnez, vous ajoutez deux manas incolores à votre réserve, et si vous perdez, rien ne se passe. Autrement dit, vous gagnerez un mana avec une probabilité de 0.5, et vous en perdrez un avec une probabilité de 0.5, et vous pouvez recommencer tant que vous avez du mana. Le problème est que vous risquez fort de vous retrouver sans mana au bout d'un moment (c'est d'ailleurs presque sûr). Par exemple, si vous avez trois terrains et Emrakul, déchirure des éons en main (qui coûte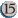
), la probabilité de vous retrouver sans mana avant d'avoir pu en obtenir suffisamment pour le lancer est 12/15 soit 80% (on verra comment le calculer plus bas)
C'est là qu'intervient le Pouce de Krark, qui permet de lancer deux pièces au lieu d'une, et de garder le lancer qu'on veut. Ainsi, on aura une probabilité de 3/4 de gagner un mana à chaque activation de Mana Screw. C'est là qu'on va commencer à faire des maths, et voir des choses amusantes se produire.
Notons e la quantité de mana que l'on souhaite obtenir, n la quantité de mana dont on dispose (avec bien entendu n<e), et p_n la probabilité d'arriver à e manas avant d'être à zéro, sachant que l'on commence avec n manas.
Une application de la formule des probabilités totales permet d'obtenir :
p_n+1 = (1/4)p_n + (3/4)p_n+2
autrement dit p_n+2 = (4/3)*[p_n+1 - (1/4)p_n]
ou p_n+2 = (4/3)p_n+1 - (1/3)p_n
On reconnaît alors une suite récurrente linéaire d'ordre 2 dont les racines de l'équation caractéristique sont 1 et 1/3. p_n est donc défini par la formule p_n = A*1^n + B*(1/3)^n
autrement dit p_n = A + B*(1/3)^n
Où A et B sont des constantes que l'on va déterminer grâce aux probabilité que l'on connaît.
p_0 est la probabilité d'arriver à e manas avant d'arriver à 0, sachant qu'on a 0 manas au départ! C'est impossible, donc p_0 = 0
p_e est la probabilité d'arriver à e manas avant d'arriver à 0, sachant qu'on a e manas au départ! C'est certain, donc p_e = 1
On a donc A+B = 0 et A+B*(1/3)^e = 1
On peut donc trouver une forme explicite de p_n :
p_n = 3^e*(3^n-1)/[3^n*(3^e-1)]
Par exemple, si on a 2 manas disponibles et Emrakul en main, on pourra le lancer avec une probabilité de 88.89%. La probabilité de pouvoir lancer une Boule de feu avec X=20 sera la même au cent-millième près.
Si on a 3 manas disponibles, cette probabilité sera d'environ 96.30%, et avec 4, elle sera de 98.77%. Les probabilités de lancer une Boule de Feu fatale sont quasi identiques là aussi.
Faire mana infini
En fait, ça ne s'arrête pas ici, car cette combo permet le plus souvent de faire mana infini. Tout d'abord, rappelons qu'à Magic, mana infini (ou jetons infini, ou quoi que ce soit d'autre infini) est un abus de langage pour désigner le fait qu'on peut produire une quantité arbitrairement grande de mana.
Rappelons la formule explicite pour p_n : p_n = 3^e*(3^n-1)/[3^n*(3^e-1)]
Si on fait tendre e vers l'infini dans cette expression, on obtient la probabilité d'obtenir toutes les valeurs possibles pour e, c'est-à-dire d'obtenir toutes les quantités de mana possibles (je vous passe les détails techniques), autrement dit, d'avoir mana infini.
Ainsi, la probabilité d'avoir mana infini avec 2 manas au départ est d'environ 88.89%, avec 3 manas, elle est de 96.30%, et avec 4 manas, de 98.77%
Sachant qu'au cas très improbables où vous ne parveniez pas à obtenir suffisamment de mana, vous pourrez recommencer au tour suivant.
Dernière remarque: dans la pratique, faire mana infini ne sert pas vraiment, on cherchera surtout à jouer la carte que l'on souhaite (Emrakul, Boule de Feu à 20...). La seule utilité de faire mana infini, c'est si votre adversaire a déjà fait quelque chose d'infini, et se retrouve par exemple avec une quantité de points de vie suffisamment grande pour qu'il soit long et fastidieux de lancer une pièce à chaque fois.
Attention: cette explication contient des maths de niveau maths sup.
Le principe est simple. Mana Screw vous permet, en payant 1 mana, de lancer une pièce. Si vous gagnez, vous ajoutez deux manas incolores à votre réserve, et si vous perdez, rien ne se passe. Autrement dit, vous gagnerez un mana avec une probabilité de 0.5, et vous en perdrez un avec une probabilité de 0.5, et vous pouvez recommencer tant que vous avez du mana. Le problème est que vous risquez fort de vous retrouver sans mana au bout d'un moment (c'est d'ailleurs presque sûr). Par exemple, si vous avez trois terrains et Emrakul, déchirure des éons en main (qui coûte
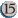), la probabilité de vous retrouver sans mana avant d'avoir pu en obtenir suffisamment pour le lancer est 12/15 soit 80% (on verra comment le calculer plus bas)C'est là qu'intervient le Pouce de Krark, qui permet de lancer deux pièces au lieu d'une, et de garder le lancer qu'on veut. Ainsi, on aura une probabilité de 3/4 de gagner un mana à chaque activation de Mana Screw. C'est là qu'on va commencer à faire des maths, et voir des choses amusantes se produire.
Notons e la quantité de mana que l'on souhaite obtenir, n la quantité de mana dont on dispose (avec bien entendu n<e), et p_n la probabilité d'arriver à e manas avant d'être à zéro, sachant que l'on commence avec n manas.
Une application de la formule des probabilités totales permet d'obtenir :
p_n+1 = (1/4)p_n + (3/4)p_n+2
autrement dit p_n+2 = (4/3)*[p_n+1 - (1/4)p_n]
ou p_n+2 = (4/3)p_n+1 - (1/3)p_n
On reconnaît alors une suite récurrente linéaire d'ordre 2 dont les racines de l'équation caractéristique sont 1 et 1/3. p_n est donc défini par la formule p_n = A*1^n + B*(1/3)^n
autrement dit p_n = A + B*(1/3)^n
Où A et B sont des constantes que l'on va déterminer grâce aux probabilité que l'on connaît.
p_0 est la probabilité d'arriver à e manas avant d'arriver à 0, sachant qu'on a 0 manas au départ! C'est impossible, donc p_0 = 0
p_e est la probabilité d'arriver à e manas avant d'arriver à 0, sachant qu'on a e manas au départ! C'est certain, donc p_e = 1
On a donc A+B = 0 et A+B*(1/3)^e = 1
On peut donc trouver une forme explicite de p_n :
p_n = 3^e*(3^n-1)/[3^n*(3^e-1)]
Par exemple, si on a 2 manas disponibles et Emrakul en main, on pourra le lancer avec une probabilité de 88.89%. La probabilité de pouvoir lancer une Boule de feu avec X=20 sera la même au cent-millième près.
Si on a 3 manas disponibles, cette probabilité sera d'environ 96.30%, et avec 4, elle sera de 98.77%. Les probabilités de lancer une Boule de Feu fatale sont quasi identiques là aussi.
Faire mana infini
En fait, ça ne s'arrête pas ici, car cette combo permet le plus souvent de faire mana infini. Tout d'abord, rappelons qu'à Magic, mana infini (ou jetons infini, ou quoi que ce soit d'autre infini) est un abus de langage pour désigner le fait qu'on peut produire une quantité arbitrairement grande de mana.
Rappelons la formule explicite pour p_n : p_n = 3^e*(3^n-1)/[3^n*(3^e-1)]
Si on fait tendre e vers l'infini dans cette expression, on obtient la probabilité d'obtenir toutes les valeurs possibles pour e, c'est-à-dire d'obtenir toutes les quantités de mana possibles (je vous passe les détails techniques), autrement dit, d'avoir mana infini.
Ainsi, la probabilité d'avoir mana infini avec 2 manas au départ est d'environ 88.89%, avec 3 manas, elle est de 96.30%, et avec 4 manas, de 98.77%
Sachant qu'au cas très improbables où vous ne parveniez pas à obtenir suffisamment de mana, vous pourrez recommencer au tour suivant.
Dernière remarque: dans la pratique, faire mana infini ne sert pas vraiment, on cherchera surtout à jouer la carte que l'on souhaite (Emrakul, Boule de Feu à 20...). La seule utilité de faire mana infini, c'est si votre adversaire a déjà fait quelque chose d'infini, et se retrouve par exemple avec une quantité de points de vie suffisamment grande pour qu'il soit long et fastidieux de lancer une pièce à chaque fois.